Perhaps we just acknowledge that math isn’t really our thing.
U.S. teenagers bombed on an international test for 15 years olds, with scores declining in math compared to 60 other countries.
Reading and writing results weren’t anything to write home about, either, assuming people could write.
On a scale of 0 to 1,000, U.S. students scored a 470 on the tests, the Associated Press reports, dropping the nation to 35th on the list of nations.
In other words, most students wouldn’t be able to figure out what percentile the nation is in now.
“The U.S. would be well served to take a hard look at the strategies used by the top-performing education systems and adapt lessons learned from them to fit the U.S. context and needs.” said Marc Tucker, president of the National Center on Education and the Economy.
“It has always been the most difficult subject for Americans,” said Andreas Schleicher, the Organization for Economic Cooperation and Development’s director for education and skills.
Students were allowed to use calculators to figure out the math problems, although the test was designed so that the need to use them was unlikely.
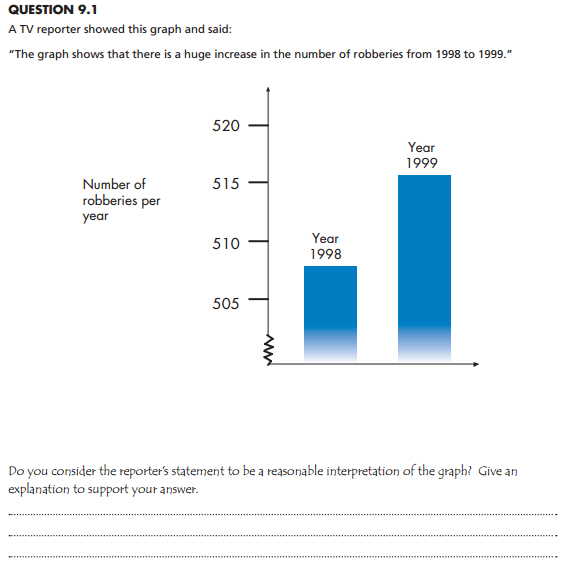
Like this one, for example:
The correct answer is it’s not a reasonable conclusion because the graphic focuses on a very small part of the graph. Another correct answer is “I don’t know” because one would need more data to determine if an increase is huge or not.
The testing agency also pointed out that “no, it’s not correct because reporters always exaggerate” is not a correct answer. That clarification was for you, America.
This one was particularly geared toward a good guess if nothing else.
The answer is 10 o’ clock for the first question. For the second, the correct answer is:
Sydney: 4:30 PM – 6:00 PM; Berlin: 7:30 AM – 9:00 AM
OR
Sydney: 7:00 AM – 8:00 AM; Berlin: 10:00 PM – 11:00 PM
Some of the questions require real math chops.
The answer is 144 and 6.
Here’s the whole sample test.
In the past, by the way, its been easy to see how Minnesota students fared against the international competition. But in the latest test, Massachusetts and North Carolina were the only states to participate as their own entities.
“We’re losing ground – a troubling prospect when, in today’s knowledge-based economy, the best jobs can go anywhere in the world. Students in Massachusetts, Maryland, and Minnesota aren’t just vying for great jobs along with their neighbors or across state lines, they must be competitive with peers in Finland, Germany, and Japan,” U.S. Education Secretary John King said.
Related: What do international tests really show about U.S. student performance? (Economic Policy Institute)