In the aftermath of the great “what color is this dress” debate, the Internet reminded us this week that it is capable of providing viral questions that actually stimulate the brain.
It’s this question: What is Cheryl’s birthday? It comes from a Facebook posting of a test question given to students in Singapore.
Singapore, we need to note, has among the highest math scores in the world. The question was part of a math olympiad for 14- and 15-year-old students, generally the top 40-percent of the country’s young mathematicians.
The students there are able to figure it out. Many of the rest of us are guessing, at least judging by the online discussions.
Vox today provides the logic that answers the question.
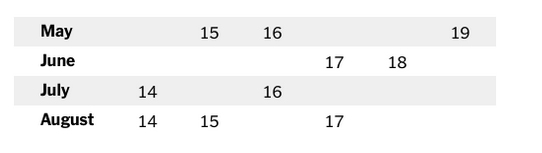
If Cheryl told Bernard she was born on the 18th or 19th, he would know her birthday right away. That’s because the 18th and 19th only show up once in Cheryl’s list of possibilities. The rest of the dates are duplicates: the 14th could be in July or August, the 15th could be in May or August, the 16th in May or July, and the 17th in June or August. But the 18th could only be in June, and the 19th only in May.
But Bernard didn’t know when Cheryl’s birthday was at first — so she wasn’t born on the 18th or 19th.
How did Albert know that Bernard didn’t know? When Cheryl told him the month, she must have said July or August, because every possible date in July and August is also in another month. If she had told Albert she was born in May or June, she might have been born on May 19 or June 18, and Albert wouldn’t be certain that Bernard was in the dark.
As soon as Albert says that, though, Bernard figures it out. How? He knows Cheryl must have told Albert her birthday is in July or August, because that’s the only way Albert can be certain that Bernard doesn’t know her birthday. Narrowing the months down to two possibilities is all it takes for him to find the answer. That means the date Cheryl gave Bernard must not be a possibility in both July and August. It’s only a possibility in one of the two months.
We already knew Cheryl’s birthday isn’t the 18th or 19th. Eliminating the dates that are in both July and August knocks out the 14th. That leaves three possible birthdays out of the original 10: July 16, August 15, or August 17.
But now Albert knows, too. That means Cheryl must not have told him she was born in August, because he’d still be confused; two of the possible dates are in August. The only remaining possibility is July 16.
The New York Times says it helps to put the answers in a table.
Now let’s examine what Albert and Bernard say. Albert goes first:
I don’t know when your birthday is, but I know Bernard doesn’t know, either.
The initial reaction is, how could Bernard know? Cheryl only whispered the day, so how could he have more information than Albert? But if Cheryl had whispered “19,” then Bernard would indeed know the exact date — May 19 — because there is only one date with 19 in it. Similarly, if Cheryl had told Bernard, “18,” then Bernard would know Cheryl’s birthday was June 18.
Thus, for this statement by Albert to be true means that Cheryl did not say to Albert, “May” or “June.” (Again, for logic puzzles, the possibility that Albert is lying or confused is off the table.) Then Bernard replies:
I didn’t know originally, but now I do.
So from Albert’s statement, Bernard now also knows that Cheryl’s birthday is not in May or June, eliminating half of the possibilities, leaving July 14, July 16, Aug. 14, Aug. 15 and Aug. 17. But Bernard now knows. If Cheryl had told him “14,” he would not know, because there would still be two possibilities: July 14 and Aug. 14. Thus we know the day is not the 14th.
Now there are only three possibilities left: July 16, Aug. 15 and Aug. 17. Albert again:
Well, now I know too!
The same logical process again: For Albert to know, the month has to be July, because if Cheryl had told him, “August,” then he would still have two possibilities: Aug. 15 and Aug. 17.
The answer is July 16.
The question also turns the Internet on its head for another reason: Comments attached to articles about the question are actually worth reading.
But maybe the best part of this is that it sparks more challenging math problems.
Sasha Volokh at Volokh Conspiracy offers this one up…
Two numbers a and b are between 2 and 99. [Note: They’re not constrained to be different from each other.]
Peter is given the product of the numbers, ab (and knows he is given the product).
Sarah is given the sum a+b (and knows she is given the sum).
They also know the numbers are between 2 and 99.
They are UVa math majors, so they are great at math and completely honorable!
Peter says, “I don’t know the numbers.”
Sarah says, “I knew you didn’t know the numbers.”
Peter then says, “I know the numbers now.”
Sarah then says, “Ah ha! I know the numbers now.”
What are the numbers?