It was a good run for Joseph Rosenfeld of Virginia, who got some fame this week for discovering an error in the Golden Ratio at Boston’s Museum of Science.
Rosenfeld noticed the apparent mistake right away.
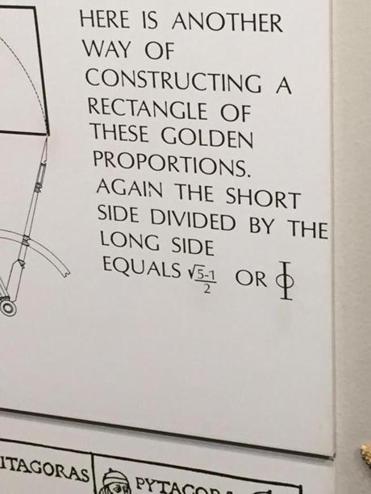
“I immediately thought it was incorrect, but I still double-checked myself on my cellphone going to Wikipedia and other websites,” Rosenfeld told the Boston Globe. Where he expected a plus sign, the museum used a minus.
The Golden Ratio says a plus b is to a as a is to b.
As Live Science explains:
The Golden ratio is a special number found by dividing a line into two parts so that the longer part divided by the smaller part is also equal to the whole length divided by the longer part. It is often symbolized using phi, after the 21st letter of the Greek alphabet. In an equation form, it looks like this:
a/b = (a+b)/a = 1.6180339887498948420 …
The ratio appears everywhere. “The length of our fingers, each section from the tip of the base to the wrist is larger than the preceding one by roughly the ratio of phi,” according to Live Science.
So why the mistake, Museum of Science?
It wasn’t a mistake, the museum now insists after first indicating it would correct the display.
The Museum of Science is thrilled at Handley High School sophomore Joseph Rosenfeld’s enthusiasm about math and our Mathematica exhibit. And it’s not at all surprising that this enterprising student noticed the minus signs because the way the Museum presents the Golden Ratio in its exhibit is in fact the less common — but no less accurate — way to present it. It’s exciting that people around the country are talking about math and science and that, in the process, we learned something too. Let’s hear it for STEM education and for Joseph Rosenfeld!
The Globe checked the museum’s math anyway.
Arthur Mattuck, an emeritus professor of mathematics at MIT, said yes. The two formulas are equal. It’s just that the Golden Ratio is normally presented the way the museum did.
“There’s no logical reason it can’t be presented the other way,” Mattuck said. “The two numbers are the same even if they look different . . . the student is just presenting the fraction upside down, in other words using the reciprocal number.”
There’s still a mystery here.
It’s contained in young Joseph’s answer to the newspaper’s question about why his favorite teacher is his favorite teacher.
“Probably Ms. Carpenter, she taught sixth grade science,” Rosenfeld said. “A lot of times I ask questions and teachers put me down or don’t answer them, but she would take time out of class to answer any questions. She was a good teacher and inspired curiosity.”
Why on earth would teachers “put down” smart students asking questions?